
| Who is it? | Mathematician, Philosopher and Logician |
| Birth Day | November 02, 1815 |
| Birth Place | Lincoln, British |
| Age | 204 YEARS OLD |
| Died On | 8 December 1864(1864-12-08) (aged 49)\nBallintemple, Cork, Ireland |
| Birth Sign | Sagittarius |
| Education | Bainbridge's Commercial Academy |
| Era | 19th-century philosophy |
| Region | Western philosophy |
| School | Mathematical foundations of computing |
| Institutions | Lincoln Mechanics' Institute Queen's College, Cork |
| Main interests | Mathematics, Logic, Philosophy of mathematics |
| Notable ideas | Boolean algebra |
George Boole, a prominent British mathematician, philosopher, and logician, is estimated to have a net worth ranging from $100,000 to $1 million in 2024. Boole contributed significantly to the advancement of mathematical logic and is best known for his work on the foundation of computer science and the development of Boolean algebra. His innovative ideas and logical principles have had a lasting impact on various fields, including computer science, artificial intelligence, and engineering. Boole's immense contributions to academia and his pioneering work in logic have solidified his position as one of the most influential figures in the history of mathematics and philosophy.


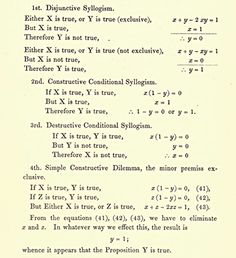


No general method for the solution of questions in the theory of probabilities can be established which does not explicitly recognise, not only the special numerical bases of the science, but also those universal laws of thought which are the basis of all reasoning, and which, whatever they may be as to their essence, are at least mathematical as to their form.
Boole was born in Lincoln, Lincolnshire, England, the son of John Boole senior (1779–1848), a shoemaker and Mary Ann Joyce. He had a primary school education, and received lessons from his father, but due to a serious decline in Business, he had little further formal and academic teaching. william Brooke, a bookseller in Lincoln, may have helped him with Latin, which he may also have learned at the school of Thomas Bainbridge. He was self-taught in modern languages. In fact, when a local newspaper printed his translation of a Latin poem, a scholar accused him of plagiarism under the pretence that he was not capable of such achievements. At age 16, Boole became the breadwinner for his parents and three younger siblings, taking up a junior teaching position in Doncaster at Heigham's School. He taught briefly in Liverpool.
Boole participated in the Mechanics Institute, in the Greyfriars, Lincoln, which was founded in 1833. Edward Bromhead, who knew John Boole through the institution, helped George Boole with mathematics books and he was given the calculus text of Sylvestre François Lacroix by the Rev. George Stevens Dickson of St Swithin's, Lincoln. Without a Teacher, it took him many years to master calculus.
Boole's views were given in four published addresses: The Genius of Sir Isaac Newton; The Right Use of Leisure; The Claims of Science; and The Social Aspect of Intellectual Culture. The first of these was from 1835, when Charles Anderson-Pelham, 1st Earl of Yarborough gave a bust of Newton to the Mechanics' Institute in Lincoln. The second justified and celebrated in 1847 the outcome of the successful campaign for early closing in Lincoln, headed by Alexander Leslie-Melville, of Branston Hall. The Claims of Science was given in 1851 at Queen's College, Cork. The Social Aspect of Intellectual Culture was also given in Cork, in 1855 to the Cuvierian Society.
From 1838 onwards Boole was making contacts with sympathetic British academic mathematicians and reading more widely. He studied algebra in the form of symbolic methods, as far as these were understood at the time, and began to publish research papers.
Boole's first published paper was Researches in the theory of analytical transformations, with a special application to the reduction of the general equation of the second order, printed in the Cambridge Mathematical Journal in February 1840 (Volume 2, no. 8, pp. 64–73), and it led to a friendship between Boole and Duncan Farquharson Gregory, the Editor of the journal. His works are in about 50 articles and a few separate publications.
In 1841 Boole published an influential paper in early invariant theory. He received a medal from the Royal Society for his memoir of 1844, On A General Method of Analysis. It was a contribution to the theory of linear differential equations, moving from the case of constant coefficients on which he had already published, to variable coefficients. The innovation in operational methods is to admit that operations may not commute. In 1847 Boole published The Mathematical Analysis of Logic, the first of his works on symbolic logic.
In 1847 Boole published the pamphlet Mathematical Analysis of Logic. He later regarded it as a flawed exposition of his logical system, and wanted An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities to be seen as the mature statement of his views. Contrary to widespread belief, Boole never intended to criticise or disagree with the main principles of Aristotle's logic. Rather he intended to systematise it, to provide it with a foundation, and to extend its range of applicability. Boole's initial involvement in logic was prompted by a current debate on quantification, between Sir william Hamilton who supported the theory of "quantification of the predicate", and Boole's supporter Augustus De Morgan who advanced a version of De Morgan duality, as it is now called. Boole's approach was ultimately much further reaching than either sides' in the controversy. It founded what was first known as the "algebra of logic" tradition.
Boole's status as Mathematician was recognised by his appointment in 1849 as the first professor of mathematics at Queen's College, Cork (now University College Cork (UCC)) in Ireland. He met his Future wife, Mary Everest, there in 1850 while she was visiting her uncle John Ryall who was Professor of Greek. They married some years later in 1855. He maintained his ties with Lincoln, working there with E. R. Larken in a campaign to reduce prostitution.
In 1855 he married Mary Everest (niece of George Everest), who later wrote several educational works on her husband's principles.
In 1857, Boole published the treatise On the Comparison of Transcendents, with Certain Applications to the Theory of Definite Integrals, in which he studied the sum of residues of a rational function. Among other results, he proved what is now called Boole's identity:
Boole completed two systematic treatises on mathematical subjects during his lifetime. The Treatise on Differential Equations appeared in 1859, and was followed, the next year, by a Treatise on the Calculus of Finite Differences, a sequel to the former work.
In fact there is the other possibility, that + should be read as disjunction. This other possibility extends from the disjoint union case, where exclusive or and non-exclusive or both give the same answer. Handling this ambiguity was an early Problem of the theory, reflecting the modern use of both Boolean rings and Boolean algebras (which are simply different aspects of one type of structure). Boole and Jevons struggled over just this issue in 1863, in the form of the correct evaluation of x + x. Jevons argued for the result x, which is correct for + as disjunction. Boole kept the result as something undefined. He argued against the result 0, which is correct for exclusive or, because he saw the equation x + x = 0 as implying x = 0, a false analogy with ordinary algebra.
In late November 1864, Boole walked, in heavy rain, from his home at Lichfield Cottage in Ballintemple to the university, a distance of three miles, and lectured wearing his wet clothes. He soon became ill, developing pneumonia. As his wife believed that remedies should resemble their cause, she put her husband to bed and poured buckets of water over him – the wet having brought on his illness. Boole's condition worsened and on 8 December 1864, he died of fever-induced pleural effusion.
Boole's work was extended and refined by a number of Writers, beginning with william Stanley Jevons. Augustus De Morgan had worked on the logic of relations, and Charles Sanders Peirce integrated his work with Boole's during the 1870s. Other significant figures were Platon Sergeevich Poretskii, and william Ernest Johnson. The conception of a Boolean algebra structure on equivalent statements of a propositional calculus is credited to Hugh MacColl (1877), in work surveyed 15 years later by Johnson. Surveys of these developments were published by Ernst Schröder, Louis Couturat, and Clarence Irving Lewis.
In 1921 the Economist John Maynard Keynes published a book on probability theory, A Treatise of Probability. Keynes believed that Boole had made a fundamental error in his definition of independence which vitiated much of his analysis. In his book The Last Challenge Problem, David Miller provides a general method in accord with Boole's system and attempts to solve the problems recognised earlier by Keynes and others. Theodore Hailperin showed much earlier that Boole had used the correct mathematical definition of independence in his worked out problems.
Boole's work and that of later logicians initially appeared to have no engineering uses. Claude Shannon attended a philosophy class at the University of Michigan which introduced him to Boole's studies. Shannon recognised that Boole's work could form the basis of mechanisms and processes in the real world and that it was therefore highly relevant. In 1937 Shannon went on to write a master's thesis, at the Massachusetts Institute of Technology, in which he showed how Boolean algebra could optimise the design of systems of electromechanical relays then used in telephone routing switches. He also proved that circuits with relays could solve Boolean algebra problems. Employing the properties of electrical switches to process logic is the basic concept that underlies all modern electronic digital computers. Victor Shestakov at Moscow State University (1907–1987) proposed a theory of electric switches based on Boolean logic even earlier than Claude Shannon in 1935 on the testimony of Soviet logicians and mathematicians Sofya Yanovskaya, Gaaze-Rapoport, Roland Dobrushin, Lupanov, Medvedev and Uspensky, though they presented their academic theses in the same year, 1938. But the first publication of Shestakov's result took place only in 1941 (in Russian). Hence, Boolean algebra became the foundation of practical digital circuit design; and Boole, via Shannon and Shestakov, provided the theoretical grounding for the Information Age.
UCC's George Boole 200 project, featured events, student outreach activities and academic conferences on Boole's legacy in the digital age, including a new edition of Desmond MacHale's 1985 biography The Life and Work of George Boole: A Prelude to the Digital Age, 2014).
Among his many innovations is his principle of wholistic reference, which was later, and probably independently, adopted by Gottlob Frege and by logicians who subscribe to standard first-order logic. A 2003 article provides a systematic comparison and critical evaluation of Aristotelian logic and Boolean logic; it also reveals the centrality of wholistic reference in Boole's philosophy of logic.
The search engine Google marked the 200th anniversary of his birth on 2 November 2015 with an algebraic reimaging of its Google Doodle.










