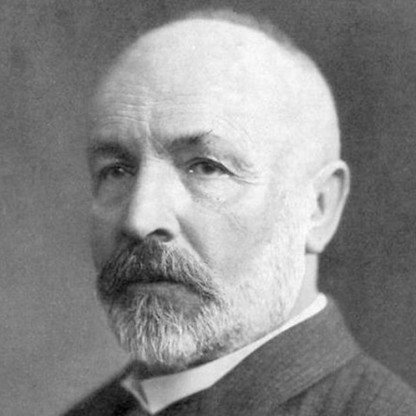
| Who is it? | Mathematician |
| Birth Day | March 03, 1845 |
| Birth Place | Saint Petersburg, Russian Empire, Russian |
| Age | 174 YEARS OLD |
| Died On | January 6, 1918(1918-01-06) (aged 72)\nHalle, Province of Saxony, German Empire |
| Birth Sign | Aries |
| Residence | Russian Empire (1845–56) German Empire (1856–1918) |
| Alma mater | Swiss Federal Polytechnic University of Berlin |
| Known for | Set theory |
| Spouse(s) | Vally Guttmann (1874-1918) |
| Awards | Sylvester Medal (1904) |
| Fields | Mathematics |
| Institutions | University of Halle |
| Thesis | De aequationibus secundi gradus indeterminatis (1867) |
| Doctoral advisor | Ernst Kummer Karl Weierstrass |
Georg Cantor, a renowned mathematician from Russia, is anticipated to have a net worth ranging from $100K to $1M in 2024. Recognized for his groundbreaking contributions to set theory and the concept of infinity, Cantor revolutionized the field of mathematics during the late 19th and early 20th centuries. He proposed groundbreaking theories like the Cantor set and introduced the notion of cardinality, which has since become fundamental in various mathematical disciplines. Cantor's extraordinary intellectual achievements have earned him a well-deserved place among the great mathematicians of history.






From his paradise that Cantor with us unfolded, we hold our breath in awe; knowing, we shall not be expelled.
Georg Cantor was born in 1845 in the western merchant colony of Saint Petersburg, Russia, and brought up in the city until he was eleven. Georg, the oldest of six children, was regarded as an outstanding Violinist. His grandfather Franz Böhm (1788–1846) (the Violinist Joseph Böhm's brother) was a well-known musician and soloist in a Russian imperial orchestra. Cantor's father had been a member of the Saint Petersburg stock exchange; when he became ill, the family moved to Germany in 1856, first to Wiesbaden, then to Frankfurt, seeking milder winters than those of Saint Petersburg. In 1860, Cantor graduated with distinction from the Realschule in Darmstadt; his exceptional skills in mathematics, trigonometry in particular, were noted. In 1862, Cantor entered the Swiss Federal Polytechnic. After receiving a substantial inheritance upon his father's death in June 1863, Cantor shifted his studies to the University of Berlin, attending lectures by Leopold Kronecker, Karl Weierstrass and Ernst Kummer. He spent the summer of 1866 at the University of Göttingen, then and later a center for mathematical research. Georg Cantor was a good student, so in 1867, he received his doctorate degree.
Cantor submitted his dissertation on number theory at the University of Berlin in 1867. After teaching briefly in a Berlin girls' school, Cantor took up a position at the University of Halle, where he spent his entire career. He was awarded the requisite habilitation for his thesis, also on number theory, which he presented in 1869 upon his appointment at Halle University.
Cantor's first ten papers were on number theory, his thesis topic. At the suggestion of Eduard Heine, the Professor at Halle, Cantor turned to analysis. Heine proposed that Cantor solve an open Problem that had eluded Peter Gustav Lejeune Dirichlet, Rudolf Lipschitz, Bernhard Riemann, and Heine himself: the uniqueness of the representation of a function by trigonometric series. Cantor solved this difficult Problem in 1869. It was while working on this Problem that he discovered transfinite ordinals, which occurred as indices n in the nth derived set Sn of a set S of zeros of a trigonometric series. Given a trigonometric series f(x) with S as its set of zeros, Cantor had discovered a procedure that produced another trigonometric series that had S1 as its set of zeros, where S1 is the set of limit points of S. If Sk+1 is the set of limit points of Sk, then he could construct a trigonometric series whose zeros are Sk+1. Because the sets Sk were closed, they contained their Limit points, and the intersection of the infinite decreasing sequence of sets S, S1, S2, S3,... formed a limit set, which we would now call Sω, and then he noticed that Sω would also have to have a set of limit points Sω+1, and so on. He had examples that went on forever, and so here was a naturally occurring infinite sequence of infinite numbers ω, ω + 1, ω + 2, ...
Between 1870 and 1872, Cantor published more papers on trigonometric series, and also a paper defining irrational numbers as convergent sequences of rational numbers. Dedekind, whom Cantor befriended in 1872, cited this paper later that year, in the paper where he first set out his celebrated definition of real numbers by Dedekind cuts. While extending the notion of number by means of his revolutionary concept of infinite cardinality, Cantor was paradoxically opposed to theories of infinitesimals of his contemporaries Otto Stolz and Paul du Bois-Reymond, describing them as both "an abomination" and "a cholera bacillus of mathematics". Cantor also published an erroneous "proof" of the inconsistency of infinitesimals.
Cantor was promoted to Extraordinary Professor in 1872 and made full Professor in 1879. To attain the latter rank at the age of 34 was a notable accomplishment, but Cantor desired a chair at a more prestigious university, in particular at Berlin, at that time the leading German university. However, his work encountered too much opposition for that to be possible. Kronecker, who headed mathematics at Berlin until his death in 1891, became increasingly uncomfortable with the prospect of having Cantor as a colleague, perceiving him as a "corrupter of youth" for teaching his ideas to a younger generation of mathematicians. Worse yet, Kronecker, a well-established figure within the mathematical community and Cantor's former professor, disagreed fundamentally with the thrust of Cantor's work ever since he intentionally delayed the publication of Cantor's first major publication in 1874. Kronecker, now seen as one of the founders of the constructive viewpoint in mathematics, disliked much of Cantor's set theory because it asserted the existence of sets satisfying certain properties, without giving specific examples of sets whose members did indeed satisfy those properties. Whenever Cantor applied for a post in Berlin, he was declined, and it usually involved Kronecker, so Cantor came to believe that Kronecker's stance would make it impossible for him ever to leave Halle.
Cantor's 1874 Crelle paper was the first to invoke the notion of a 1-to-1 correspondence, though he did not use that phrase. He then began looking for a 1-to-1 correspondence between the points of the unit square and the points of a unit line segment. In an 1877 letter to Richard Dedekind, Cantor proved a far stronger result: for any positive integer n, there exists a 1-to-1 correspondence between the points on the unit line segment and all of the points in an n-dimensional space. About this discovery Cantor wrote to Dedekind: "Je le vois, mais je ne le crois pas!" ("I see it, but I don't believe it!") The result that he found so astonishing has implications for geometry and the notion of dimension.
In 1878, Cantor submitted another paper to Crelle's Journal, in which he defined precisely the concept of a 1-to-1 correspondence and introduced the notion of "power" (a term he took from Jakob Steiner) or "equivalence" of sets: two sets are equivalent (have the same power) if there exists a 1-to-1 correspondence between them. Cantor defined countable sets (or denumerable sets) as sets which can be put into a 1-to-1 correspondence with the natural numbers, and proved that the rational numbers are denumerable. He also proved that n-dimensional Euclidean space R has the same power as the real numbers R, as does a countably infinite product of copies of R. While he made free use of countability as a concept, he did not write the word "countable" until 1883. Cantor also discussed his thinking about dimension, stressing that his mapping between the unit interval and the unit square was not a continuous one.
Between 1879 and 1884, Cantor published a series of six articles in Mathematische Annalen that together formed an introduction to his set theory. At the same time, there was growing opposition to Cantor's ideas, led by Kronecker, who admitted mathematical concepts only if they could be constructed in a finite number of steps from the natural numbers, which he took as intuitively given. For Kronecker, Cantor's hierarchy of infinities was inadmissible, since accepting the concept of actual infinity would open the door to paradoxes which would challenge the validity of mathematics as a whole. Cantor also introduced the Cantor set during this period.
In 1881, Cantor's Halle colleague Eduard Heine died, creating a vacant chair. Halle accepted Cantor's suggestion that it be offered to Dedekind, Heinrich M. Weber and Franz Mertens, in that order, but each declined the chair after being offered it. Friedrich Wangerin was eventually appointed, but he was never close to Cantor.
In 1882, the mathematical correspondence between Cantor and Richard Dedekind came to an end, apparently as a result of Dedekind's declining the chair at Halle. Cantor also began another important correspondence, with Gösta Mittag-Leffler in Sweden, and soon began to publish in Mittag-Leffler's journal Acta Mathematica. But in 1885, Mittag-Leffler was concerned about the philosophical nature and new terminology in a paper Cantor had submitted to Acta. He asked Cantor to withdraw the paper from Acta while it was in proof, writing that it was "... about one hundred years too soon." Cantor complied, but then curtailed his relationship and correspondence with Mittag-Leffler, writing to a third party:
Cantor's 1883 paper reveals that he was well aware of the opposition his ideas were encountering:
After Cantor's 1884 hospitalization, there is no record that he was in any sanatorium again until 1899. Soon after that second hospitalization, Cantor's youngest son Rudolph died suddenly on December 16 (Cantor was delivering a lecture on his views on Baconian theory and william Shakespeare), and this tragedy drained Cantor of much of his passion for mathematics. Cantor was again hospitalized in 1903. One year later, he was outraged and agitated by a paper presented by Julius König at the Third International Congress of Mathematicians. The paper attempted to prove that the basic tenets of transfinite set theory were false. Since the paper had been read in front of his daughters and colleagues, Cantor perceived himself as having been publicly humiliated. Although Ernst Zermelo demonstrated less than a day later that König's proof had failed, Cantor remained shaken, and momentarily questioning God. Cantor suffered from chronic depression for the rest of his life, for which he was excused from teaching on several occasions and repeatedly confined in various sanatoria. The events of 1904 preceded a series of hospitalizations at intervals of two or three years. He did not abandon mathematics completely, however, lecturing on the paradoxes of set theory (Burali-Forti paradox, Cantor's paradox, and Russell's paradox) to a meeting of the Deutsche Mathematiker–Vereinigung in 1903, and attending the International Congress of Mathematicians at Heidelberg in 1904.
In 1888, Cantor published his correspondence with several Philosophers on the philosophical implications of his set theory. In an extensive attempt to persuade other Christian thinkers and authorities to adopt his views, Cantor had corresponded with Christian Philosophers such as Tilman Pesch and Joseph Hontheim, as well as Theologians such as Cardinal Johannes Franzelin, who once replied by equating the theory of transfinite numbers with pantheism. Cantor even sent one letter directly to Pope Leo XIII himself, and addressed several pamphlets to him.
In 1889, Cantor was instrumental in founding the German Mathematical Society and chaired its first meeting in Halle in 1891, where he first introduced his diagonal argument; his reputation was strong enough, despite Kronecker's opposition to his work, to ensure he was elected as the first President of this society. Setting aside the animosity Kronecker had displayed towards him, Cantor invited him to address the meeting, but Kronecker was unable to do so because his wife was dying from injuries sustained in a skiing accident at the time. Georg Cantor was also instrumental in the establishment of the first International Congress of Mathematicians, which was held in Zürich, Switzerland, in 1897.
In 1891, he published a paper containing his elegant "diagonal argument" for the existence of an uncountable set. He applied the same idea to prove Cantor's theorem: the cardinality of the power set of a set A is strictly larger than the cardinality of A. This established the richness of the hierarchy of infinite sets, and of the cardinal and ordinal arithmetic that Cantor had defined. His argument is fundamental in the solution of the Halting Problem and the proof of Gödel's first incompleteness theorem. Cantor wrote on the Goldbach conjecture in 1894.
Cantor extended his work on the absolute infinite by using it in a proof. Around 1895, he began to regard his well-ordering principle as a theorem and attempted to prove it. In 1899, he sent Dedekind a proof of the equivalent aleph theorem: the cardinality of every infinite set is an aleph. First, he defined two types of multiplicities: consistent multiplicities (sets) and inconsistent multiplicities (absolutely infinite multiplicities). Next he assumed that the ordinals form a set, proved that this leads to a contradiction, and concluded that the ordinals form an inconsistent multiplicity. He used this inconsistent multiplicity to prove the aleph theorem. In 1932, Zermelo criticized the construction in Cantor's proof.
In a letter written by Georg Cantor to Paul Tannery in 1896 (Paul Tannery, Memoires Scientifique 13 Correspondence, Gauthier-Villars, Paris, 1934, p. 306), Cantor states that his paternal grandparents were members of the Sephardic Jewish community of Copenhagen. Specifically, Cantor states in describing his father: "Er ist aber in Kopenhagen geboren, von israelitischen Eltern, die der dortigen portugisischen Judengemeinde..." ("He was born in Copenhagen of Jewish (lit: "Israelite") parents from the local Portuguese-Jewish community.")
The Continuum hypothesis, introduced by Cantor, was presented by David Hilbert as the first of his twenty-three open problems in his address at the 1900 International Congress of Mathematicians in Paris. Cantor's work also attracted favorable notice beyond Hilbert's celebrated encomium. The US Philosopher Charles Sanders Peirce praised Cantor's set theory, and, following public lectures delivered by Cantor at the first International Congress of Mathematicians, held in Zurich in 1897, Hurwitz and Hadamard also both expressed their admiration. At that Congress, Cantor renewed his friendship and correspondence with Dedekind. From 1905, Cantor corresponded with his British admirer and translator Philip Jourdain on the history of set theory and on Cantor's religious ideas. This was later published, as were several of his expository works.
Cantor avoided paradoxes by recognizing that there are two types of multiplicities. In his set theory, when it is assumed that the ordinals form a set, the resulting contradiction only implies that the ordinals form an inconsistent multiplicity. On the other hand, Bertrand Russell treated all collections as sets, which leads to paradoxes. In Russell's set theory, the ordinals form a set, so the resulting contradiction implies that the theory is inconsistent. From 1901 to 1903, Russell discovered three paradoxes implying that his set theory is inconsistent: the Burali-Forti paradox (which was just mentioned), Cantor's paradox, and Russell's paradox. Russell named paradoxes after Cesare Burali-Forti and Cantor even though neither of them believed that they had found paradoxes.
The harsh criticism has been matched by later accolades. In 1904, the Royal Society awarded Cantor its Sylvester Medal, the highest honor it can confer for work in mathematics. David Hilbert defended it from its critics by declaring:
In 1908, Zermelo published his axiom system for set theory. He had two motivations for developing the axiom system: eliminating the paradoxes and securing his proof of the well-ordering theorem. Zermelo had proved this theorem in 1904 using the axiom of choice, but his proof was criticized for a variety of reasons. His response to the criticism included his axiom system and a new proof of the well-ordering theorem. His axioms support this new proof, and they eliminate the paradoxes by restricting the formation of sets.
In 1911, Cantor was one of the distinguished foreign scholars invited to attend the 500th anniversary of the founding of the University of St. Andrews in Scotland. Cantor attended, hoping to meet Bertrand Russell, whose newly published Principia Mathematica repeatedly cited Cantor's work, but this did not come about. The following year, St. Andrews awarded Cantor an honorary doctorate, but illness precluded his receiving the degree in person.
Cantor retired in 1913, living in poverty and suffering from malnourishment during World War I. The public celebration of his 70th birthday was canceled because of the war. In June 1917, he entered a sanatorium for the last time and continually wrote to his wife asking to be allowed to go home. Georg Cantor had a fatal heart attack on January 6, 1918, in the sanatorium where he had spent the last year of his life.
In 1923, John von Neumann developed an axiom system that eliminates the paradoxes by using an approach similar to Cantor's—namely, by identifying collections that are not sets and treating them differently. Von Neumann stated that a class is too big to be a set if it can be put into one-to-one correspondence with the class of all sets. He defined a set as a class that is a member of some class and stated the axiom: A class is not a set if and only if there is a one-to-one correspondence between it and the class of all sets. This axiom implies that these big classes are not sets, which eliminates the paradoxes since they cannot be members of any class. Von Neumann also used his axiom to prove the well-ordering theorem: Like Cantor, he assumed that the ordinals form a set. The resulting contradiction implies that the class of all ordinals is not a set. Then his axiom provides a one-to-one correspondence between this class and the class of all sets. This correspondence well-orders the class of all sets, which implies the well-ordering theorem. In 1930, Zermelo defined Models of set theory that satisfy von Neumann's axiom.
There were documented statements, during the 1930s, that called this Jewish ancestry into question:
The difficulty Cantor had in proving the continuum hypothesis has been underscored by later developments in the field of mathematics: a 1940 result by Gödel and a 1963 one by Paul Cohen together imply that the continuum hypothesis can neither be proved nor disproved using standard Zermelo–Fraenkel set theory plus the axiom of choice (the combination referred to as "ZFC").
Until the 1970s, the chief academic publications on Cantor were two short monographs by Schönflies (1927) – largely the correspondence with Mittag-Leffler – and Fraenkel (1930). Both were at second and third hand; neither had much on his personal life. The gap was largely filled by Eric Temple Bell's Men of Mathematics (1937), which one of Cantor's modern biographers describes as "perhaps the most widely read modern book on the history of mathematics"; and as "one of the worst". Bell presents Cantor's relationship with his father as Oedipal, Cantor's differences with Kronecker as a quarrel between two Jews, and Cantor's madness as Romantic despair over his failure to win acceptance for his mathematics, and fills the picture with stereotypes. Grattan-Guinness (1971) found that none of these claims were true, but they may be found in many books of the intervening period, owing to the absence of any other narrative. There are other legends, independent of Bell – including one that labels Cantor's father a foundling, shipped to Saint Petersburg by unknown parents. A critique of Bell's book is contained in Joseph Dauben's biography. Writes Dauben:
(the rest of the quote is finished by the very first quote above). In Men of Mathematics, Eric Temple Bell described Cantor as being "of pure Jewish descent on both sides," although both parents were baptized. In a 1971 article entitled "Towards a Biography of Georg Cantor," the British Historian of mathematics Ivor Grattan-Guinness mentions (Annals of Science 27, pp. 345–391, 1971) that he was unable to find evidence of Jewish ancestry. (He also states that Cantor's wife, Vally Guttmann, was Jewish).
Cantor introduced fundamental constructions in set theory, such as the power set of a set A, which is the set of all possible subsets of A. He later proved that the size of the power set of A is strictly larger than the size of A, even when A is an infinite set; this result soon became known as Cantor's theorem. Cantor developed an entire theory and arithmetic of infinite sets, called cardinals and ordinals, which extended the arithmetic of the natural numbers. His notation for the cardinal numbers was the Hebrew letter 
Cantor also believed that his theory of transfinite numbers ran counter to both materialism and determinism – and was shocked when he realized that he was the only faculty member at Halle who did not hold to deterministic philosophical beliefs.










