| Who is it? | Mathematician and Astronomer |
| Birth Place | Bhinmal, Indian |
| Died On | c. 668 CE |
| Residence | Bhillamāla Ujjain |
| Known for | Zero Modern number system Brahmagupta's theorem Brahmagupta's identity Brahmagupta's problem Brahmagupta-Fibonacci identity Brahmagupta's interpolation formula Brahmagupta's formula |
| Fields | Mathematics, astronomy |
Brahmagupta, the renowned mathematician and astronomer from India, is estimated to have a net worth ranging from $100,000 to $1 million in 2024. Known for his exceptional contributions to the fields of mathematics and astronomy during the 7th century, Brahmagupta's groundbreaking work played a crucial role in the development of the Indian numerical system and trigonometry. His profound understanding of planetary motion and astronomical calculations elevated the scientific knowledge of his time. Today, Brahmagupta is remembered as one of the most influential scholars in the history of mathematics and astronomy in India.
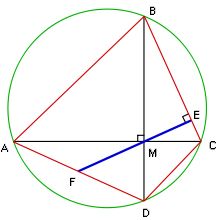
The difference between rupas, when inverted and divided by the difference of the unknowns, is the unknown in the equation. The rupas are [subtracted on the side] below that from which the square and the unknown are to be subtracted.
So Brahmagupta uses 3 as a "practical" value of π, and as an "accurate" value of π. The error in this "accurate" value is less than 1%.
The Historian of science George Sarton called him "one of the greatest Scientists of his race and the greatest of his time." Brahmagupta's mathematical advances were carried on further by Bhāskara II, a lineal descendant in Ujjain, who described Brahmagupta as the ganaka-chakra-chudamani (the GEM of the circle of mathematicians). Prithudaka Svamin wrote commentaries on both of his works, rendering difficult verses into simpler language and adding illustrations. Lalla and Bhattotpala in the 8th and 9th centuries wrote commentaries on the Khanda-khadyaka. Further commentaries continued to be written into the 12th century.
In 665 Brahmagupta devised and used a special case of the Newton–Stirling interpolation formula of the second-order to interpolate new values of the sine function from other values already tabulated. The formula gives an estimate for the value of a function f at a value a + xh of its argument (with h > 0 and −1 ≤ x ≤ 1) when its value is already known at a − h, a and a + h.
